This tutorial includes an implementation of a decision network in Python. A decision network (influence diagram) is used for AI decisions in uncertain environments. A decision network includes nodes, edges (arcs) and probabilistic information to support decision making when outcomes is uncertain.
A decision network (DN) is a bayesian network with the addition of nodes for actions and utilities. A DN is used to create utility-based agents with information about the current state, possible actions, results of actions and utilities of states.
A decision network is created as a directed acyclic graph (DAG) with decision nodes, chance nodes and utility nodes. A chance node (ellips) includes different outcomes with probabilities, an utility node (diamond) includes information about the utility for a certain decision and a decision node (rectangle) represent an outcome for a decision (Yes/No). Nodes are connected to each other with arcs or edges.
You can modify evidences for chance nodes, change utility and make inference in a decision network to get answers about the best decisions to make in order to maximize the expected utility.
Problem and Libraries
I am going to create a decision network for an oil drilling problem, the influence diagram includes decisions to test for oil and to drill for oil. I am using pyAgrum to create the decision network and to make inference from the network, cairosvg is used to convert an svg-image to a png-image.
Influence Diagram
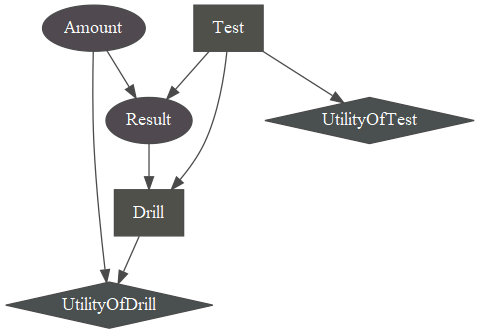
The decision network includes a chance node for amount of oil and a chance node for test result. This network includes utility nodes for drilling and testing, and decision nodes for test and drilling. Probabilities is added as conditional probability tables (CPT:s). A network can be saved to an bifxml-file and a network can be loaded from a bifxml-file. Output from a run is shown below the code.
# Import libraries
import pyAgrum as gum
import pyAgrum.lib.notebook as gnb
import cairosvg
# The main entry point for this module
def main():
# Load a decision network
#oil=gum.loadID('data\\OilWildcater.bifxml')
# Create a decision network
model = gum.InfluenceDiagram()
# Add a decision node for test
test = gum.LabelizedVariable('Test','Test for oil',2)
test.changeLabel(0,'Yes')
test.changeLabel(1,'No')
model.addDecisionNode(test)
# Add a decision node for drill
drill = gum.LabelizedVariable('Drill','Drill for oil',2)
drill.changeLabel(0,'Yes')
drill.changeLabel(1,'No')
model.addDecisionNode(drill)
# Add a chance node for result of test
result = gum.LabelizedVariable('Result','Result of test',4)
result.changeLabel(0,'NoS')
result.changeLabel(1,'OpS')
result.changeLabel(2,'ClS')
result.changeLabel(3,'NoR')
model.addChanceNode(result)
# Add a chance node for oil amount
amount = gum.LabelizedVariable('Amount','Oil amount',3)
amount.changeLabel(0,'Dry')
amount.changeLabel(1,'Wet')
amount.changeLabel(2,'Soak')
model.addChanceNode(amount)
# Add an utility node for testing
ut_test = gum.LabelizedVariable('UtilityOfTest','Utility of Testing',1)
model.addUtilityNode(ut_test)
# Add an utility node for drilling
ut_drill = gum.LabelizedVariable('UtilityOfDrill','Utility of Drilling',1)
model.addUtilityNode(ut_drill)
# Add connections between nodes
model.addArc(model.idFromName('Test'), model.idFromName('Result'))
model.addArc(model.idFromName('Test'), model.idFromName('UtilityOfTest'))
model.addArc(model.idFromName('Test'), model.idFromName('Drill'))
model.addArc(model.idFromName('Amount'), model.idFromName('Result'))
model.addArc(model.idFromName('Amount'), model.idFromName('UtilityOfDrill'))
model.addArc(model.idFromName('Result'), model.idFromName('Drill'))
model.addArc(model.idFromName('Drill'), model.idFromName('UtilityOfDrill'))
# Add utilities
model.utility(model.idFromName('UtilityOfTest'))[{'Test':'Yes'}]=-10
model.utility(model.idFromName('UtilityOfTest'))[{'Test':'No'}]=0
model.utility(model.idFromName('UtilityOfDrill'))[{'Drill':0}]=[[-70],[0],[50]]
model.utility(model.idFromName('UtilityOfDrill'))[{'Drill':1}]=[[0],[200],[0]]
# Add CPT:s
model.cpt(model.idFromName('Amount'))[0]=0.5 # Dry
model.cpt(model.idFromName('Amount'))[1]=0.3 # Wet
model.cpt(model.idFromName('Amount'))[2]=0.2 # Soak
model.cpt(model.idFromName('Result'))[{'Test':'Yes'}]=[[0.6, 0.3, 0.1, 0], # Dry
[0.3, 0.4, 0.3, 0], # Wet
[0.1, 0.4, 0.5, 0]] # Soak
model.cpt(model.idFromName('Result'))[{'Test':'No'}]=[[0, 0, 0, 1], # Dry
[0, 0, 0, 1], # Wet
[0, 0, 0, 1]] # Soak
# Save the model
gum.saveBN(model, 'data\\oil.bifxml')
# Get and save an influence diagram
svg = gnb.getInfluenceDiagram(model)
cairosvg.svg2png(bytestring=svg,write_to='plots\\drill_network.png')
# Create an inference model
ie = gum.InfluenceDiagramInference(model)
# Make an inference with default evidence
ie.makeInference()
print('--- Inference with default evidence ---')
print(ie.displayResult())
print('Best decision for Test: {0}'.format(ie.getBestDecisionChoice(model.idFromName('Test'))))
print('Best decision for Drill: {0}'.format(ie.getBestDecisionChoice(model.idFromName('Drill'))))
print('Maximum Expected Utility (MEU) : {0}'.format(ie.getMEU()))
print()
# Print variable 3
print('--- Variable 3 ---')
print(model.variable(3))
print()
# Erase all evidence
ie.eraseAllEvidence()
# Erase all evidence and set new evidences
ie.setEvidence({3:[0,0,1]})
# Make an inference with evidence
ie.makeInference()
print('--- Inference with evidence ---')
print(ie.displayResult())
print('Best decision for Test: {0}'.format(ie.getBestDecisionChoice(model.idFromName('Test'))))
print('Best decision for Drill: {0}'.format(ie.getBestDecisionChoice(model.idFromName('Drill'))))
print('Maximum Expected Utility (MEU) : {0}'.format(ie.getMEU()))
print()
# Tell python to run main method
if __name__ == "__main__": main()--- Inference with default evidence ---
max EU :
<UtilityOfTest:0|UtilityOfDrill:0> :: 60
Best choices :
- Decision Drill<Yes,No> : No
- Decision Test<Yes,No> : No
Best decision for Test: 1
Best decision for Drill: 1
Maximum Expected Utility (MEU) : 60.0
--- Variable 3 ---
Amount<Dry,Wet,Soak>
--- Inference with evidence ---
max EU :
<UtilityOfTest:0|UtilityOfDrill:0> :: 10
Best choices :
- Decision Drill<Yes,No> : Yes
- Decision Test<Yes,No> : No
Best decision for Test: 1
Best decision for Drill: 0
Maximum Expected Utility (MEU) : 10.0