I am going to solve two problems with constraint programming in this tutorial. Constraint Programming (CP) is a flexible technique that can be used to solve constraint satisfaction problems (CSP) with more or less feasible solutions. CP-problems can be modeled with arbitrary constraints. CP focuses most on variables and constraints, it has less focus on the objective function.
Constraint programming is used for planning, scheduling and assignments. I am going to solve a job shop scheduling problem and a house building scheduling problem in this tutorial. CP is used to find a feasible solutions, but I will try to find optimal solutions. I am using Python and the ortools library from Google in this tutorial.
Job Shop Scheduling Problem
A job shop performs multiple jobs in multiple machines (Job Shop Problem) and the objective is to find a schedule for each machine that minimizes the time it takes for all the jobs to be completed. A job has multiple tasks that must be executed in order and each machine can only handle one task at a time. Output from a run is shown below the code.
# Import libraries
import collections
import ortools.sat.python.cp_model
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
# This class represent a task
class Task:
# Create a new task
def __init__(self, start:object, interval:object, end:object):
# Set values for instance variables
self.start = start
self.interval = interval
self.end = end
# This class represent an assignment
class Assignment:
# Create a new assignment
def __init__(self, job_id:int, task_id:int, start:int, duration:int):
# Set values for instance variables
self.job_id = job_id
self.task_id = task_id
self.start = start
self.duration = duration
# Sort
def __lt__(self, other):
return self.start + self.duration < other.start + other.duration
# Print
def __repr__(self):
return ('(Job: {0}, Task: {1}, Start: {2}, End: {3})'.format(self.job_id, self.task_id, self.start, self.start + self.duration))
# The main entry point for this module
def main():
# Input data: Task = (machine_id, duration)
jobs = [[(0, 3), (1, 2), (2, 2)], # Job0
[(0, 2), (2, 1), (1, 4)], # Job1
[(1, 4), (2, 3)] # Job2
]
# Variables
machine_count = 3
tasks = {}
intervals = collections.defaultdict(list)
assignments = collections.defaultdict(list)
# Compute horizon dynamically (sum of all durations)
horizon = sum(task[1] for job in jobs for task in job)
# Create a model
model = ortools.sat.python.cp_model.CpModel()
# Loop jobs
for job_id, job in enumerate(jobs):
# Loop tasks in a job
for task_id, task in enumerate(job):
# Variables
machine_id = task[0]
duration = task[1]
suffix = '_{0}_{1}'.format(job_id, task_id)
# Create model variables
start = model.NewIntVar(0, horizon, 'start' + suffix)
end = model.NewIntVar(0, horizon, 'end' + suffix)
interval = model.NewIntervalVar(start, duration, end, 'interval' + suffix)
# Add a task
tasks[job_id, task_id] = Task(start, interval, end)
# Add an interval for the machine
intervals[machine_id].append(interval)
# Add no-overlap constraints
# A machine can only work with 1 task at a time
for machine in range(machine_count):
model.AddNoOverlap(intervals[machine])
# Add precedence constraints
# Tasks in a job must be performed in the specified order
for job_id, job in enumerate(jobs):
# Loop tasks in a job
for task_id in range(len(job) - 1):
# Add a precedence constraint
model.Add(tasks[job_id, task_id + 1].start >= tasks[job_id, task_id].end)
# Create an objective function
objective = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(objective, [tasks[job_id, len(job) - 1].end for job_id, job in enumerate(jobs)])
model.Minimize(objective)
# Create a solver
solver = ortools.sat.python.cp_model.CpSolver()
# Set a time limit of 30 seconds.
solver.parameters.max_time_in_seconds = 30.0
# Solve the problem
status = solver.Solve(model)
# Print output if the solution is optimal
if (status == ortools.sat.python.cp_model.OPTIMAL):
# Loop jobs
for job_id, job in enumerate(jobs):
# Loop tasks in a job
for task_id, task in enumerate(job):
# Add an assignment
machine_id = task[0]
start = solver.Value(tasks[job_id, task_id].start)
assignments[machine_id].append(Assignment(job_id, task_id, start, task[1]))
# Create bars and sort assignments
bars = []
for machine in range(machine_count):
assignments[machine].sort()
bar_tasks = []
for ass in assignments[machine]:
bar_tasks.append((ass.start, ass.duration))
bars.append(bar_tasks)
# Print the solution
print('--- Final solution ---\n')
print('Optimal Schedule Length: {0}\n'.format(solver.ObjectiveValue()))
print('Schedules:')
for machine in range(machine_count):
print(machine,':', *assignments[machine])
print()
# Plot gantt chart
fig, gnt = plt.subplots(figsize=(12, 8))
fig.suptitle('Gantt Chart', fontsize=16)
gnt.set_xlabel('Time')
gnt.set_ylabel('Machines')
gnt.set_yticks([12, 22, 32])
gnt.set_yticklabels(['0', '1', '2'])
gnt.grid(True)
# Loop bars
for i in range(len(bars)):
gnt.broken_barh(bars[i], (10 + i * 10, 4), facecolors=('tab:orange', 'tab:green', 'tab:red'))
j = 0
for x1, x2 in bars[i]:
gnt.text(x=x1 + x2/2, y= 12 + i * 10, s=j, ha='center', va='center', color='white')
j += 1
# Create a legend
labels = []
labels.append(mpatches.Patch(color='tab:orange', label='Task 0'))
labels.append(mpatches.Patch(color='tab:green', label='Task 1'))
labels.append(mpatches.Patch(color='tab:red', label='Task 2'))
plt.legend(handles=labels, loc=4)
# Show or save the plot
#plt.show()
plt.savefig('plots\\schedule-gantt.png')
# Tell python to run main method
if __name__ == '__main__': main()--- Final solution ---
Optimal Schedule Length: 11.0
Schedules:
0 : (Job: 0, Task: 0, Start: 0, End: 3) (Job: 1, Task: 0, Start: 3, End: 5)
1 : (Job: 2, Task: 0, Start: 0, End: 4) (Job: 0, Task: 1, Start: 4, End: 6) (Job: 1, Task: 2, Start: 7, End: 11)
2 : (Job: 1, Task: 1, Start: 5, End: 6) (Job: 0, Task: 2, Start: 6, End: 8) (Job: 2, Task: 1, Start: 8, End: 11)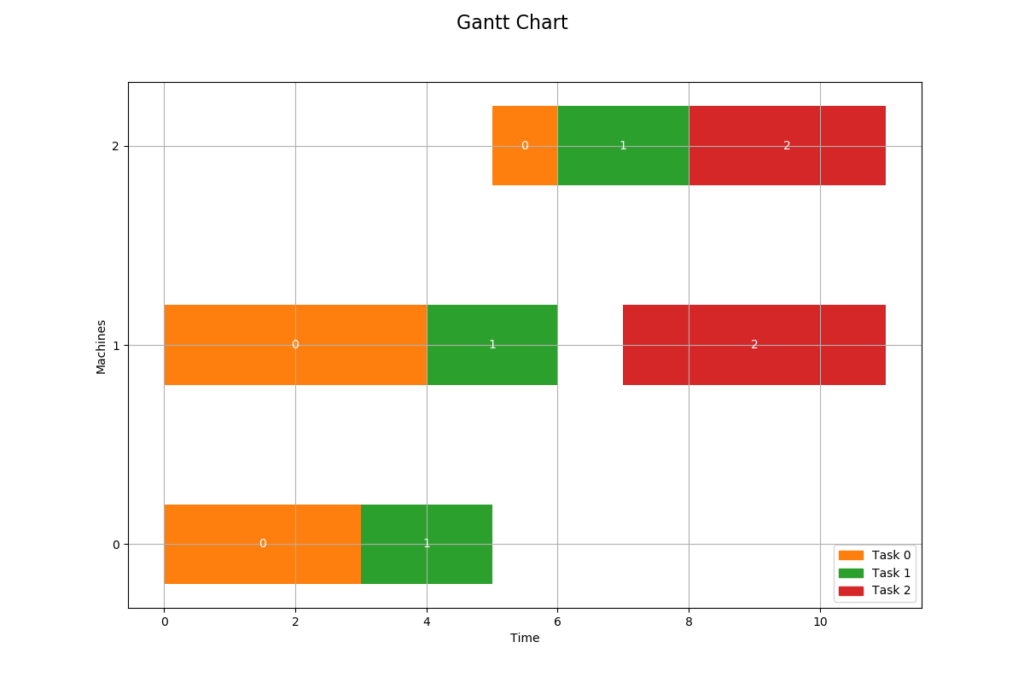
Build Five Houses
This is a scheduling problem (House Building) in which 3 workers should build 5 houses before a specified deadline. Each worker has a certain skill for each job and the objective is to maximize the total skill for the entire project. Output from a run is shown below the code, jobs in the gantt chart can overlap each other.
# Import libraries
import collections
import ortools.sat.python.cp_model
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
# This class represent a job
class Job:
# Create a new job
def __init__(self, duration:int, skills:[]):
# Set values for instance variables
self.duration = duration
self.skills = skills
# This class represent a task
class Task:
# Create a new task
def __init__(self, start:object, end:object):
# Set values for instance variables
self.start = start
self.end = end
# This class represent an assignment
class Assignment:
# Create a new assignment
def __init__(self, job:int, worker:str, start:int, duration:int, skill:int):
# Set values for instance variables
self.job = job
self.worker = worker
self.start = start
self.duration = duration
self.skill = skill
# Sort
def __lt__(self, other):
return self.start + self.duration < other.start + other.duration
# Print
def __repr__(self):
return ('{0}: {1}: {2}, Start: {3}, End: {4}'.format(str.title(self.job), self.worker, self.skill, self.start, self.start + self.duration))
# The main entry point for this module
def main():
# Variables
count_houses = 5
deadline = 400
workers = ['Joe', 'Jack', 'Jim']
jobs = {}
tasks = {}
worker_tasks = {}
precedences = []
intervals = collections.defaultdict(list)
assignments = collections.defaultdict(list)
objective = []
# Add jobs
jobs['masonry'] = Job(35, [9, 5, 0])
jobs['carpentry'] = Job(15, [7, 0, 5])
jobs['plumbing'] = Job(40, [0, 7, 0])
jobs['ceiling'] = Job(15, [5, 8, 0])
jobs['roofing'] = Job(5, [6, 7, 0])
jobs['painting'] = Job(10, [0, 9, 6])
jobs['windows'] = Job(5, [8, 0, 5])
jobs['facade'] = Job(10, [5, 5, 0])
jobs['garden'] = Job(5, [5, 5, 9])
jobs['moving'] = Job(5, [6, 0, 8])
# Add precedences
precedences.append(('masonry', 'carpentry'))
precedences.append(('masonry', 'plumbing'))
precedences.append(('masonry', 'ceiling'))
precedences.append(('carpentry', 'roofing'))
precedences.append(('ceiling', 'painting'))
precedences.append(('roofing', 'windows'))
precedences.append(('roofing', 'facade'))
precedences.append(('plumbing', 'facade'))
precedences.append(('roofing', 'garden'))
precedences.append(('plumbing', 'garden'))
precedences.append(('windows', 'moving'))
precedences.append(('facade', 'moving'))
precedences.append(('garden', 'moving'))
precedences.append(('painting', 'moving'))
# Create a model
model = ortools.sat.python.cp_model.CpModel()
# Loop houses
for house_id in range(count_houses):
# Loop jobs
for job_id, job in jobs.items():
# Variables
suffix = '_{0}_{1}'.format(house_id, job_id)
# Create model variables
start = model.NewIntVar(0, deadline, 'start' + suffix)
end = model.NewIntVar(0, deadline, 'end' + suffix)
# Add a task
tasks[house_id, job_id] = Task(start, end)
# Loop workers
allocation = []
for worker in range(len(workers)):
if(job.skills[worker] > 0):
suffix = '_{0}_{1}_{2}'.format(house_id, job_id, worker)
presence = model.NewBoolVar('precence' + suffix)
interval = model.NewOptionalIntervalVar(start, job.duration, end, presence, 'interval' + suffix)
worker_tasks[house_id, job_id, worker] = presence
intervals[worker].append(interval)
allocation.append(presence)
objective.append(job.skills[worker] * presence)
# One and only one worker must be assigned to a job
model.Add(sum(allocation) == 1)
# Add precedence constraints
for i, j in precedences:
model.Add(tasks[house_id, j].start >= tasks[house_id, i].end)
# Avoid overlapping between tasks of each worker
for worker in range(len(workers)):
model.AddNoOverlap(intervals[worker])
# Create an objective function
model.Maximize(sum(objective))
# Create a solver
solver = ortools.sat.python.cp_model.CpSolver()
# Set a time limit of 30 seconds.
solver.parameters.max_time_in_seconds = 30.0
# Solve the problem
status = solver.Solve(model)
# Print output if the solution is optimal
if (status == ortools.sat.python.cp_model.OPTIMAL):
# Loop houses
for house_id in range(count_houses):
# Loop jobs
for job_id, task in jobs.items():
start = solver.Value(tasks[house_id, job_id].start)
worker = 0
for w in range(len(workers)):
if(task.skills[w] > 0 and solver.Value(worker_tasks[house_id, job_id, w]) == 1):
worker = w
break
duration = task.duration
assignments[house_id].append(Assignment(job_id, workers[worker], start, duration, task.skills[worker]))
# Create bars and sort assignments
bars = []
for house_id in range(count_houses):
assignments[house_id].sort()
bar_tasks = []
for ass in assignments[house_id]:
bar_tasks.append((ass.start, ass.duration))
bars.append(bar_tasks)
# Print the solution
print('--- Final solution ---\n')
print('Optimal Total Skill: {0}\n'.format(solver.ObjectiveValue()))
for house_id in range(count_houses):
print('House:', house_id + 1)
print(*assignments[house_id], sep='\n')
print()
print()
# Plot gantt chart
fig, gnt = plt.subplots(figsize=(16, 8))
fig.suptitle('Gantt Chart', fontsize=16)
gnt.set_xlabel('Time')
gnt.set_ylabel('Houses')
gnt.set_yticks([12, 22, 32, 42, 52])
gnt.set_yticklabels(['1', '2', '3', '4', '5'])
gnt.grid(True)
# Loop bars
for i in range(len(bars)):
gnt.broken_barh(bars[i], (10 + i * 10, 4), facecolors=('tab:blue', 'tab:orange', 'tab:green', 'tab:red', 'tab:purple', 'tab:brown', 'tab:pink', 'tab:gray', 'tab:olive', 'tab:cyan'))
# Create a legend
labels = []
labels.append(mpatches.Patch(color='tab:blue', label='Masonry'))
labels.append(mpatches.Patch(color='tab:orange', label='Carpentry'))
labels.append(mpatches.Patch(color='tab:green', label='Plumbing'))
labels.append(mpatches.Patch(color='tab:red', label='Ceiling'))
labels.append(mpatches.Patch(color='tab:purple', label='Roofing'))
labels.append(mpatches.Patch(color='tab:brown', label='Painting'))
labels.append(mpatches.Patch(color='tab:pink', label='Windows'))
labels.append(mpatches.Patch(color='tab:gray', label='Facade'))
labels.append(mpatches.Patch(color='tab:olive', label='Garden'))
labels.append(mpatches.Patch(color='tab:cyan', label='Moving'))
plt.legend(handles=labels, loc=4)
# Show or save the plot
#plt.show()
plt.savefig('plots\\workers-gantt.png')
# Tell python to run main method
if __name__ == '__main__': main()--- Final solution ---
Optimal Total Skill: 385.0
House: 1
Masonry: Joe: 9, Start: 0, End: 35
Carpentry: Joe: 7, Start: 35, End: 50
Plumbing: Jack: 7, Start: 35, End: 75
Ceiling: Jack: 8, Start: 75, End: 90
Roofing: Jack: 7, Start: 90, End: 95
Windows: Joe: 8, Start: 95, End: 100
Garden: Jim: 9, Start: 95, End: 100
Painting: Jack: 9, Start: 95, End: 105
Facade: Joe: 5, Start: 100, End: 110
Moving: Jim: 8, Start: 110, End: 115
House: 2
Masonry: Joe: 9, Start: 50, End: 85
Carpentry: Joe: 7, Start: 110, End: 125
Plumbing: Jack: 7, Start: 105, End: 145
Ceiling: Jack: 8, Start: 145, End: 160
Roofing: Jack: 7, Start: 160, End: 165
Windows: Joe: 8, Start: 165, End: 170
Garden: Jim: 9, Start: 165, End: 170
Painting: Jack: 9, Start: 165, End: 175
Facade: Joe: 5, Start: 170, End: 180
Moving: Jim: 8, Start: 180, End: 185
House: 3
Masonry: Joe: 9, Start: 125, End: 160
Carpentry: Joe: 7, Start: 180, End: 195
Plumbing: Jack: 7, Start: 175, End: 215
Ceiling: Jack: 8, Start: 215, End: 230
Roofing: Jack: 7, Start: 230, End: 235
Windows: Joe: 8, Start: 235, End: 240
Garden: Jim: 9, Start: 235, End: 240
Painting: Jack: 9, Start: 235, End: 245
Facade: Joe: 5, Start: 240, End: 250
Moving: Jim: 8, Start: 250, End: 255
House: 4
Masonry: Joe: 9, Start: 195, End: 230
Carpentry: Joe: 7, Start: 250, End: 265
Plumbing: Jack: 7, Start: 245, End: 285
Ceiling: Jack: 8, Start: 285, End: 300
Roofing: Jack: 7, Start: 300, End: 305
Windows: Joe: 8, Start: 305, End: 310
Garden: Jim: 9, Start: 305, End: 310
Painting: Jack: 9, Start: 305, End: 315
Facade: Joe: 5, Start: 310, End: 320
Moving: Jim: 8, Start: 320, End: 325
House: 5
Masonry: Joe: 9, Start: 265, End: 300
Carpentry: Joe: 7, Start: 320, End: 335
Plumbing: Jack: 7, Start: 315, End: 355
Ceiling: Jack: 8, Start: 355, End: 370
Roofing: Jack: 7, Start: 370, End: 375
Windows: Joe: 8, Start: 375, End: 380
Garden: Jim: 9, Start: 375, End: 380
Painting: Jack: 9, Start: 375, End: 385
Facade: Joe: 5, Start: 380, End: 390
Moving: Jim: 8, Start: 390, End: 395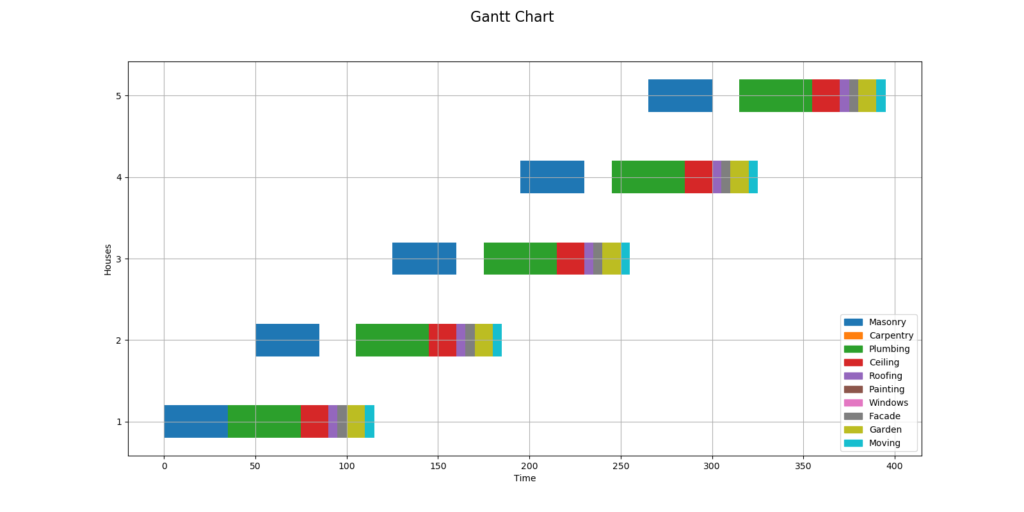
Hi, In example provided for building 5 different houses, is it possible to add different duration of tasks for different house? for example: duration for masonry for house_1 is 35, for house_2 is 45, for house_3 is 30. please suggest.
Can somebody help me with the program that uses a Constraint Satisfaction Problem (CSP) formulation to find possible
schedules of daily activities. The activities should be scheduled within an eight hour block (9am to 5pm), one for each hour, such that
every hour is scheduled for some activity. The following activities are needed to be scheduled:
• Work (4 hours total, 2 must be consecutive)
• Lunch (1 hour, but not before 10am, and not after 2pm)
• Exercise (1 hour, but must be after lunch)
• Shopping (1 hour)
• Reading, Meeting, or Cleaning (any one of these, for 1 hour)